Understanding Derivatives: The Foundation of Calculus

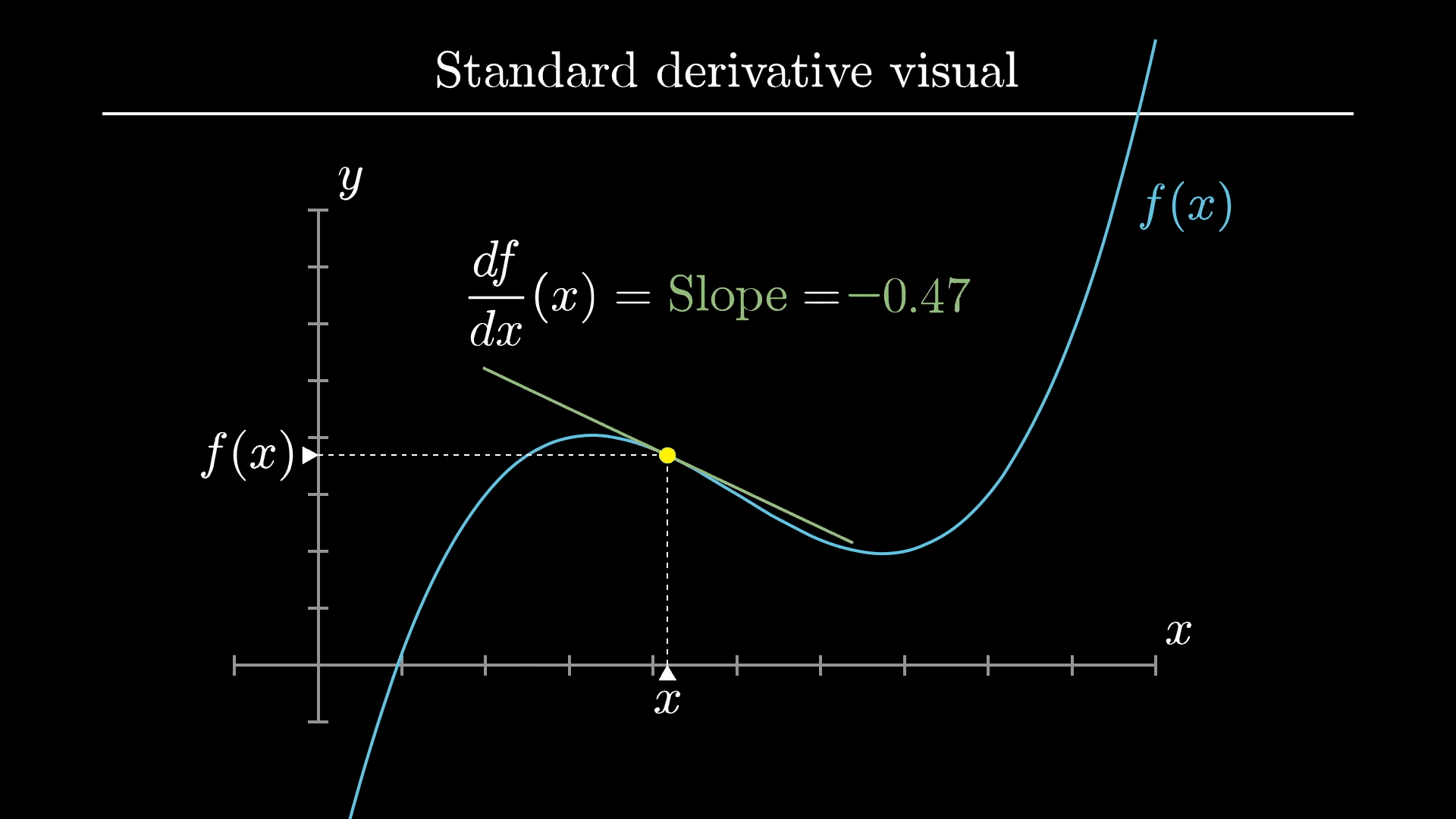
Introduction to Derivatives

Derivatives are one of the most fundamental concepts in calculus, representing the rate of change of a function with respect to a variable. In real-world terms, derivatives help us understand how quickly things are changing, whether it's the speed of a moving car or the rate of growth of a population.

Mathematically, the derivative of a function ( f(x) ) is defined as:

f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h}

This definition gives us a precise way to calculate the instantaneous rate of change of ( f(x) ) at any point ( x ).

Applications of Derivatives

One of the most common applications of derivatives is in physics, where they describe how quantities such as velocity and acceleration change over time. For instance, if ( s(t) ) represents the position of an object at time ( t ), the derivative ( s'(t) ) gives the object's velocity, and the second derivative ( s''(t) ) gives its acceleration:

v(t) = \frac{ds(t)}{dt}, \quad a(t) = \frac{dv(t)}{dt} = \frac{d^2 s(t)}{dt^2}

Derivatives are also used in optimization problems, where we seek to find the maximum or minimum values of a function. These are found by setting the derivative equal to zero and solving for the critical points:

f'(x) = 0

Higher-Order Derivatives

Beyond the first derivative, higher-order derivatives provide further insights into the behavior of a function. For example, the second derivative tells us about the concavity of a function, helping us determine whether a critical point is a local maximum, minimum, or a point of inflection.

f''(x) > 0 \quad \text{(local minimum)}

f''(x) < 0 \quad \text{(local maximum)}

Conclusion

Derivatives are a cornerstone of calculus with wide-ranging applications in science, engineering, economics, and beyond. From analyzing motion to optimizing systems, understanding how things change is critical to solving real-world problems.